Os gregos estavam fascinados pelos números e acreditavam que eles tinham propriedades mágicas. Além disso, a civilização grega tinha uma enorme preocupação com a estética, tendo muitos dos arquitetos, artesãos e artistas da época baseado suas obras nos princípios geométricos.
Um destes princípios gira em torno de uma constante real algébrica irracional denotada pela letra grega φ. Trata-se de um problema que foi resolvido pela primeira vez por Euclides (300 a.C.), onde q razão entre dois números (a e b) é igual a soma destes, dividido pelo primeiro (a).

Essa razão foi denominada em 1509, por Fra Luca Pacioli, como proporção divina. Podemos resolver esse problema de forma a encontrar o valor desta proporção.
A razão áurea é definida algebricamente como::
A equação da direita mostra que  , o que pode ser substituído na parte esquerda, resultando em:
, o que pode ser substituído na parte esquerda, resultando em:
Cancelando b em ambos os lados, temos:
Multiplicando ambos os lados por  , resulta:
, resulta:
Finalmente, subtraindo 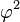 de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos:
de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos:
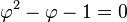 , que é uma equação quadrática da forma:
, que é uma equação quadrática da forma:-
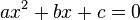 , em que
, em que 
Resolvendo essa equação, temos que :

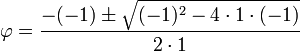


A única solução positiva dessa equação quadrática é a seguinte:
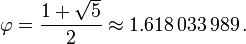 , que é o número
, que é o número  .
.
Mas o que esse número tem de especial?
Já na Grécia antiga sabia-se que muitas das figuras geométricas preservavam essa proporção. Entre elas o pentágono regular e o icosaedro, um sólido de 20 faces formadas por triângulos equiláteros, sendo cada um destes triângulos formado pela ligação de um das arestas de retângulos áureos. Veja na figura abaixo:

Não é difícil verificar a fascinação que os gregos tinham por esta proporção, se olharmos para uma foto das ruínas do Partenon. É possível verificar que ele foi todo desenhado utilizando-se retângulos áureos.

Aproximadamente 1500 anos depois de Euclides, Leonardo de Pisa (1175-1250), um matemático italiano, mais conhecido como Fibonacci ("Filho de boa natureza"), propôs um problema cuja solução era uma sequência de números (0,1,1,2,3,5,8,13,...). Mais 500 anos se passaram até que Johannes Kepler (1571-1630) tenha verificado uma conexão entre a série de Fibonacci e a razão áurea.
A série de Fibonacci é aquela em que cada número da sequência é gerado pela soma dos dois anteriores. Kepler mostrou que a razão dessa sequência se aproxima cada vez mais da razão áurea:
2/1 = 2
3/2 = 1,5
5/3 = 1,66
8/5 = 1,6
13/8 = 1,625
21/13 = 1,615...
Desde então, manifestações da série de Fibonacci e do número áureo tem aparecido em todos os lugares. Como é o caso de várias áreas de estudo da Biologia. Uma destas manifestações aparece na concha de certos moluscos.

A forma dessa concha é conhecida na matemática como espiral logarítmica. Sua construção pode ser realizada partindo de um quadrado de lado 1 e colocando outro idêntico ao seu lado. Em seguida, para completar a figura, adiciona-se mais um quadrado, sendo esse agora de lado 2. Consequentemente, o próximo quadrado a ser adicionado tem que ter lado 3 (2+1), e o próximo terá lado 5 (3+2). Continuando a acrescentar mais quadrados, percebe-se que a sequência formada pelos lados dos quadrados é dada pela série de Fibonacci. Ligando-se os vértices desses quadrados na forma de um arco de circunferência, a figura gerada é uma espiral logarítmica, idêntica ao formato da concha do molusco da figura.

Outra área da Biologia em que é observado a proporção divina é na Botânica, num ramo de pesquisa que estuda a disposição das folhas nos talos das plantas e recebe o nome de Filotaxia. Na maioria dos casos, percebe-se que com o intuito de maximizar a captação de luz, a disposição das folhas segue uma trajetória ascendente na forma de uma hélice:
Uma importante propriedade no estudo da Filotaxia é medida da seguinte forma: Partindo de uma determinada folha do talo, seguindo de forma ascendente até a próxima folha de mesma orientação, o número de folhas encontradas nesse caminho chamamos de n. Nesse mesmo trajeto, também podemos contar o número de voltas dadas no talo, chamamos esse número de m. A caracterização ou divergência das plantas e dada pela razão n/m. Vamos considerar agora a sequência de Fibonacci como {Fi}, tal que: F1=1 F2=1, F3=2, F4=5, F6=8... O surpreendente na Filotaxia é que a caracterização das plantas, na maioria dos casos, é dada justamente por elementos da série de Fibonacci, do tipo Fi/F(i+2). No caso do Llorón a caracterização seria F4/F6.
Ainda na Botânica, podemos nos fazer as seguintes perguntas: Por que as margaridas tem geralmente 34, 55, ou 89 pétalas? Por que as pinhas tem 8 diagonais num sentido e 13 no outro? Por que o girassol tem 21 espirais para um lado e 34 para o outro?
A verdade é que os biólogos não estão de acordo sobre qual a razão para toda essa "numerologia". Entretanto, é espantoso que todos esses números tenham relação com a série de Fibonacci e, consequentemente, a razão áurea.
Leonardo da Vinci, obviamente, não ficaria de fora dessa história, e em sua obra mais famosa, La Gioconda (Monalisa), podem ser observados os retângulos áureos:
Ainda na Biologia, também a Anatomia humana está cheia destas proporções divinas. Por exemplo: A razão entre a altura de uma pessoa e a distância do umbigo até o solo, a distância entre o ombro e as pontas dos dedos dividida pela distância entre o cotovelo e a pontas dos dedos, a relação entre as falanges dos dedos dos pés com a das mãos, a relação entre a altura da cabeça e sua largura. Todas estas frações nos levam ao número φ.
O que de divino realmente tem esse número? Com certeza não será a ciência que dará a resposta, mas é realmente surpreendente a quantidade de situações em que essa razão é encontrada e, por isso, é fácil de entender o porquê da proporção divina ter encantando tanto aos gregos, a cerca de 2,5 mil anos atrás, e encanta tantas pessoas, inclusive cientistas, até hoje.
Mais curiosidades sobre a razão áurea podem ser encontradas na wikipédia.
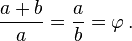
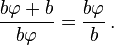






Comentários
Postar um comentário